
이번 포스팅에서 알아볼 내용은 정렬 ( Sort ) 알고리즘과 시간복잡도입니다.
정렬 종류의 기준
- 원소들의 교환 횟수에 따른 계산 복잡도
- 메모리 사용량
- 재귀성의 포함 여부와 둘다 포함하는 경우
- 안정성
- 비교 정렬 여부
- 알고리즘의 종류 ( 직렬, 정렬 )
- 순응성 ( 입력을 미리 정하는 것이 실행 시간에 영향을 미치는 정도 )

시간 복잡도가 O(n²)인 정렬
- 버블 정렬 ( Bubble Sort )
- 선택 정렬 ( Selection Sort )
- 삽입 정렬 ( Insertion Sort )
시간복잡도가 O(n log n)인 정렬
- 병합 정렬/ 합병 정렬 ( Merge Sort )
- 힙 정렬 ( Heap Sort )
- 퀵 정렬 ( Quick Sort )
- 트리 정렬 ( Tree Sort )
그 밖의 정렬
- 카운팅 정렬 ( Counting Sort : O(n+k), k는 데이터의 최댓값 )
- 기수 정렬 ( Radix Sort : O(kn), k는 데이터의 자릿수 )
시간 복잡도가 O(n²)인 정렬 알고리즘을 Javascript로 구현하기
버블 정렬
const arr = [5, 4, 3, 2, 1]
const bubbleSort = (arr) => {
for (let i = 0; i < arr.length; i++) {
let temp;
for (let j = 0; j < arr.length - 1 - i; j++){
if (arr[j] > arr[ j + 1]) {
temp = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = temp
}
}
console.log(`버블 정렬 ${i} 회전 : ${arr}`)
if (!temp) {
break
}
}
return arr
}
console.log(bubbleSort(arr))
temp라는 변수를 만들어 arr[ j ]와 arr[j + 1]의 값을 비교하여 arr[ j ]가 더 크면 자리를 교환합니다.
각 회전을 끝내고 temp 변수가 undefined 상태라면 정렬이 다 되었다는 것으로 반복문을 종료합니다.
선택 정렬
const arr = [5, 4, 3, 2, 1]
const selectionSort = (arr) => {
for (let i = 0; i < arr.length; i++) {
let minIdx = i
for (let j = i + 1; j < arr.length; j++) {
if (arr[minIdx] > arr[j]) {
minIdx = j
}
}
if (minIdx !== i) {
let temp = arr[minIdx]
arr[minIdx] = arr[i]
arr[i] = temp
}
console.log(`선택 정렬의 ${i}회전 : ${arr}`)
}
return arr
}
console.log(selectionSort(arr))
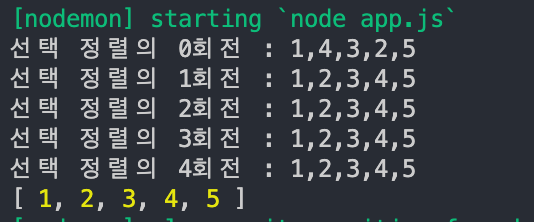
선택 정렬은 항상 첫 번째 자리를 기준으로 정렬하며 첫 번째 자리를 가장 작은 값이라 가정하여 minIdx변수에 i를 담습니다.
i + 1 번째 자리부터 순회하며 arr[ i ]보다 값을 비교해 검사하고 검사가 끝나면 minIdx값이 i와 같지 않다면 해당 값과 i번째 값을 교환합니다.
삽입 정렬
const arr = [5, 4, 3, 2, 1]
const selectionSort = (arr) => {
for (let i = 1; i < arr.length; i++) {
let currentValue = arr[i]
let leftValue = i - 1
while (leftValue >= 0 && arr[leftValue] > currentValue) {
arr[leftValue + 1] = arr[leftValue]
arr[leftValue] = currentValue
currentValue = arr[leftValue]
leftValue--
}
console.log(`삽입 정렬의 ${i}회전 : ${arr}`)
}
return arr
}
console.log(selectionSort(arr))
currentValue 변수에 현재의 데이터를 저장하고 leftValue변수에 현재 인덱스의 - 1의 값을 넣습니다.
반복문으로 leftValue 변수가 0보다 크거나 같으며 arr[ leftValue ]가 currentValue보다 큰 경우에 해당 두 데이터를 교환하고
currentValue 변수에 arr[leftValue]를 담아 leftValue값에 -1의 값을 더합니다.
1번째 데이터를 뽑아 0번째 데이터와 비교한 후 0번째 데이터가 더 크면 해당 값을 교환합니다.
다음엔 교환한 1번째 데이터와 0번째 데이터를 비교합니다.
0번째 데이터가 1번째 데이터보다 크다면 다시 값을 교환합니다.
원본 데이터가 정렬이 되어있는 경우에는 while 반복문이 실행되지 않으므로 O(n)의 시간복잡도가 성립합니다.
이번 포스팅으로 시간복잡도가 O(n²)인 정렬에 대해 알아보았습니다.