앞서 포스팅한 스택 ( Stack ), 큐 ( Queue )등은 자료구조에서 선형 구조라고 합니다.
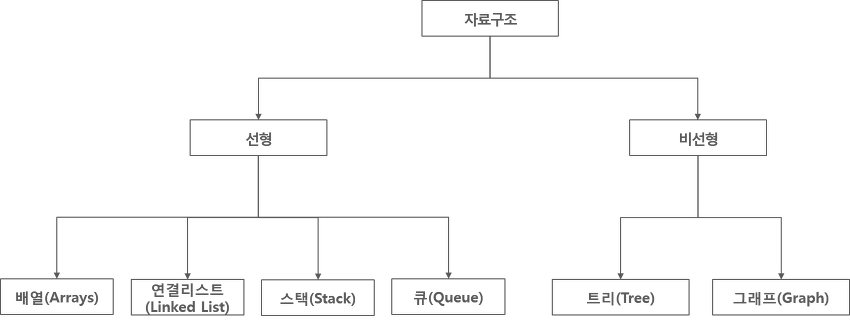
이번 포스팅에서는 알고리즘 중 비선형 구조를 갖고있는 Tree에 대해 알아보겠습니다.
Tree 자료구조는 그래프의 한 종류로
Tree란 어떠한 노드의 집합으로 노드들은 서로 다른 자식을 가지며
이 때 각자의 노드는 재사용되지 않는 구조를 갖는다.
Tree에는 여러가지 특징들이 존재합니다.
- Tree의 서로 다른 임의의 두 노드에 대해 두 노드를 연결하는 경로는 유일하다.
- Tree에는 사이클을 가지는 노드 집합이 존재하지 않는다.
- Tree에는 반드시 하나의 Root가 존재합니다 ( 최상위 노드, 부모 노드가 존재하지 않는 노드 )

선형 구조란?? ( Linear )
자료를 구성하는 데이터를 순차적으로 나열시킨 형태를 의미합니다.
선형 구조는 자료를 저장하고 자료를 꺼내는 것에 초점이 맞춰져 있고, 비선형구조는 표현에 초점이 맞춰져 있습니다.
그렇다면 비선형 구조란 무엇일까요??

비선형 구조 ( Non-Linear )
비선형 구조란 하나의 자료 뒤 혹은 안에 여러개의 자료가 존재할 수 있는 것을 의미합니다.
이러한 모형이 계층적인 구조를 갖는 것을 Tree( 트리 )라고 할 수 있습니다.

Tree 관련 용어
노드 ( Node ) : 트리의 구성요소에 해당하는 모든 요소 ( 루트, x, y, 리프 )
루트 노드 ( Root Node ) : 트리 구조에서 최상위에 존재하는 레벨 0의 노드를 루트 노드라고 합니다.
( 즉, 하나의 트리 구조에서는 하나의 루트가 존재합니다. )
리프 노드 ( Leaf Node ) : 트리의 가장 아랫부분에 위치하는 노드를 리프( Leaf )라고 합니다. 가장 아랫부분의 의미는
물리적으로 가장 아래가 아닌 더이상 뻗어 나갈 수 없는 마지막 노드의 위치를 의미합니다.
( 리프 노드는 가장 하위 노드로 자식 노드를 갖지 않습니다. )
안쪽 노드 : 루트를 포함해 리프를 제외한 노드를 안쪽 노드라고 합니다. ( 그림의 x, y )
형제 노드 : 같은 부모를 가지는 자식 노드들을 말합니다.
깊이 ( depth ) : Tree 구조에서 부모로 부터 자식 순으로 이동할 때, 깊이 ( depth )가 1씩 증가하며 따라서 형제 노드들은 같은 깊이 ( depth )를 가지며 루트 노드 ( Root Node )의 깊이는 0이 됩니다.
레벨 ( Level ) : Root로부터 얼마나 떨어져 있는지에 대한 값을 레벨( Level )이라고 합니다.
( 루트의 레벨은 0이며 루트로부터 가지가 하나씩 아래로 뻗어나갈 때 마다 레벨이 1씩 증가합니다. )
차수 : 노드가 갖는 자식의 수를 차수 ( degree )라고 합니다. 모든 노드의 차수가 n 이하인 트리를 n진 트리라고 합니다.
( X의 차수는 2이며 Y의 차수는 3입니다. 위의 그림은 Node의 자식이 모두 3개 이하이므로 3진 트리라고 합니다. )
서브 트리 ( sub-tree ) : 큰 트리 ( 전체 )에 속하는 작은 트리를 말합니다.
높이 ( Height ) : 트리의 최고 레벨 ( 위의 그림에서는 높이가 3입니다. )
널 트리 ( null-tree ) : 노드 혹은 가지가 없는 트리를 널-트리라고 합니다.

이진트리

노드가 왼쪽 자식과 오른쪽 자식을 갖는 트리를 이진 트리 ( Binary Tree )라고 합니다.
각각의 노드의 자식은 2개 이하여야 합니다.
완전이진트리
최상위 노드 ( 루트 )부터 노드가 채워져 있으면서 같은 레벨에서 왼쪽부터 오른쪽 순서 방향으로 노드가 채워져 있는
이진 트리를 완전 이진 트리 ( Complete Binary Tree )라고 합니다.
마지막 레벨을 제외한 레벨은 노드를 가득 채운다.
마지막 레벨은 왼쪽에서 오른쪽 방향으로 채우며 반드시 끝까지 채울 필요는 없습니다.
완전 이진 트리에서 너비 우선 탐색을 하며 각 노드에 0, 1, 2... 값을 주면 배열에 저장하는 인덱스와 일대일로 대응합니다.
n개의 노드를 저장할 수 있는 완전이진트리의 높이는 log n을 갖습니다.
이진검색트리( Binary Search Tree )
이진검색트리는 이진트리가 다음 조건을 만족하였을때 입니다.
- 어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 노드 N의 키 값보다 작아야합니다.
- 오른쪽 서브 트리 노드의 키 값은 노드 N의 키 값보다 커야합니다.
- 같은 키 값을 갖는 노드는 존재하지 않습니다.

이진검색트리를 구현한 예시 그림입니다.
Node 5를 기준으로 보았을 때 왼쪽 Sub-Tree-Node( 4, 1 )은 모두 5보다 작습니다.
오른쪽 서브 트리 노드( 7, 6, 9)는 모두 5보다 큽니다.
이때 이진검색트리를 중위순회 ( Inorder )하게 된다면
다음과 같이 키 값의 오름차순으로 노드를 얻을 수 있다.
1 -> 4 -> 5 -> 6 -> 7 -> 9 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18
갑자기 중위순회?
순회 ( Traversal )
이진 트리를 순회한다는 것은 이진 트리에 속하는 모든 노드를 한 번씩 방문하여 노드가 가지고 있는 데이터를
목적에 맞게 처리하는 것을 의미합니다.
트리를 사용하는 목적은 트리의 노드에 자료를 저장하고 필요에 따라서 이 자료를 처리하기 위함입니다.
따라서 트리가 가지고 있는 자료를 순차적으로 순회하는 것은 이진 트리에서 중요한 연산입니다.
선형 구조의 스택과 큐는 자료를 저장하기 때문에 순회하는 방법이 한 가지씩 ( LIFO / FIFO )뿐이었지만
트리는 여러 가지 순서로 자료에 접근할 수 있습니다.
순회 방법에는 최상위 노드 ( Root )를 방문하는 순서에 따라
- 전위 순회 ( Preorder ) : VLR
- 중위 순회 ( Inorder ) : LVR
- 후위 순회 ( Postorder ) : LRV
로 나눌 수 있습니다. ( V : Visited, L : Left, R : Right )
이진 트리에서 각 서브 트리 또한 이진 트리이므로 같은 방법을 적용해 순회할 수 있습니다.
문제의 구조( 이진 -> 이진)는 같지만 크기가 작아지는 경우 "순환"을 적용할 수 있다는 것입니다.
전위 순회 ( Pre-Order Traversal : VLR )

전위 순회의 방문 순서 ( VLR : 루트로 부터 왼쪽 부터 오른쪽 까지 순회하는 방법입니다. )
중위 순회 ( In-Order Traversal : LVR )

중위 순회의 방문 순서 ( LVR : 왼쪽 맨 하위 노드로 부터 시작해 루트를 거쳐 오른쪽 맨 하위 노드를 순회하는 방법입니다. )
후위 순회 ( Postorder Traversal : LRV )

후위 순회의 방문 순서 ( LRV : 왼쪽 맨 하위 노드부터 시작해 루트를 거치지 않으며 오른쪽 노드를 순회하고 루트를 방문하는 방법입니다. )

레벨 순회 ( Level Traversal )
각 노드를 레벨 순으로 검사하는 순회 방법입니다.
이전의 순회 방법들은 순환 호출을 함으로 간접적으로 스택을 사용하는 반면에
레벨 순회는 큐를 사용하는 순회 방법입니다.
레벨 순회 코드는 큐에 하나라도 노드가 있다면 계속 반복하는 코드로 구성되어 있습니다.
레벨 순회의 의사 코드
levelOrder ( root )
// 큐를 초기화
initialize queue;
// 트리 루트가 Null인 경우 종료
if ( root = null ) then return;
// 트리 루트의 루트 노드를 큐에 Enqueue합니다.
enqueue ( queue, root );
// 큐가 비어있는 상태가 될 때 까지 계속해서 반복
while isEmpty( queue ) != TRUE do
// 큐에서 맨 처음에 있는 노드를 x로 가져옵니다. ( Dequeue )
x <- dequeue ( queue );
// x의 데이터 값을 출력한다
print x -> data;
// x의 왼쪽 노드 ( 자식 )이 Null이 아닌 경우
if ( x-> left != NULL) then
// 큐에 Enqueue
enqueue (queue, x -> left);
// x의 오른쪽 자식이 NULL이 아닌 경우
if( x-> right != null) then
// 큐에 Enqueue
enqueue( queue, x -> right );
실제 구현하기 전에 의사 코드로 작성하는 것은 사고를 명확히 정립함으로써 프로그램 설계 시 많은 도움이 됩니다.
- 코드 검토를 쉽게 함으로써 지속적인 프로그램 개선에 도움이 됩니다.
- 코드를 전부 작성한 후에 수정하는 것보다 의사코드 설계 단계에서 미리 오류를 수정함으로써 코드 수정을 용이하게 만들어준다. ( 즉, 유지보수가 쉬워집니다. )
- 개발 경험이 늘어갈 수록 다양한 언어를 배우게 되면 언어의 문법이 헷갈릴 수 있습니다. 이런 상황에 의사코드로 먼저 논리를 정리한 다음, 문법만 해당 언어에 맞게 작성하면 되는 쉬운 방법을 제시합니다.
간단한 프로그램을 구현할 때는 필요성을 체감하기 어려울 수 있지만, 점차 큰 프로그램을 만들면서 필요성을 느끼게 될 것입니다.
필요성을 느끼기 이전에 미리 의사코드를 사용해 정리하는 습관을 만든다면 구현 시간을 단축하고 논리적인 사고력을 기르는데 도움이 될 수 있다는 것을 말씀드리고 싶습니다. ( 출처 : https://medium.com/quantum-ant/%ED%8A%B8%EB%A6%AC-tree-cec69cfddb14 )